MO417 - Questão para a prova oral

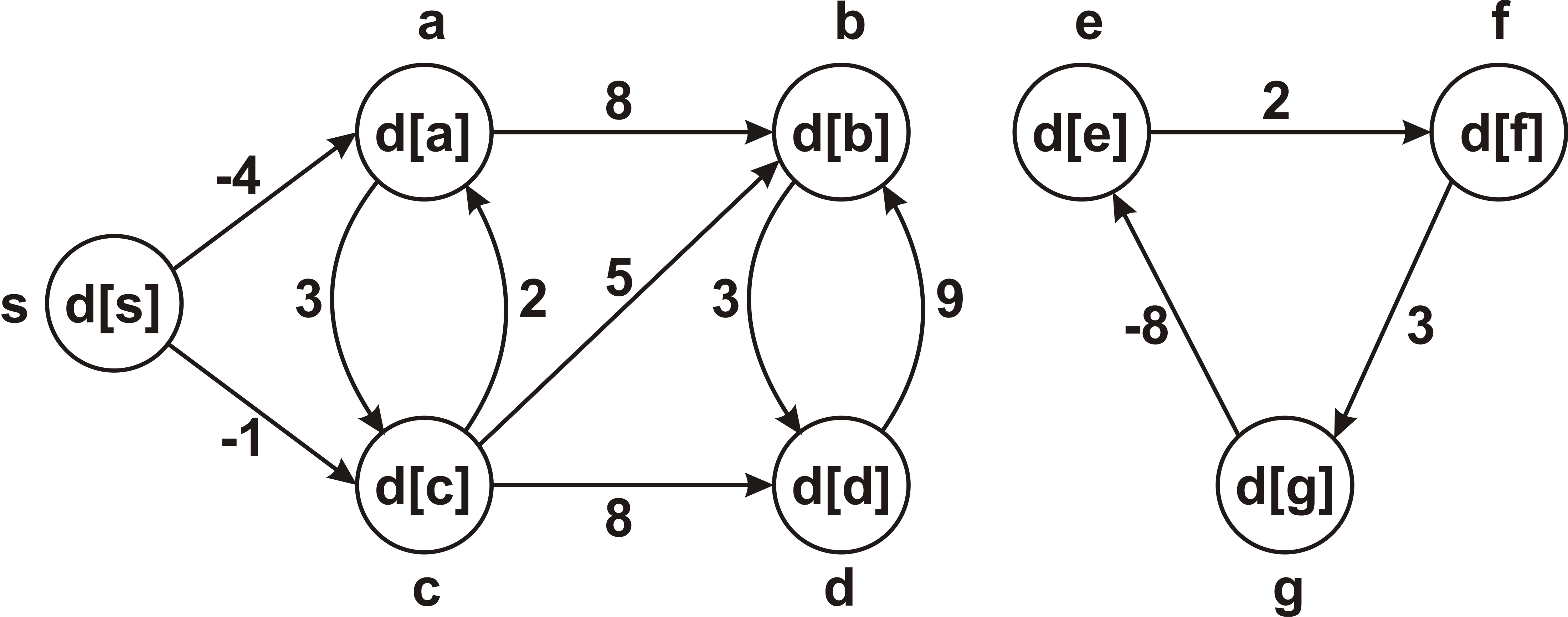
Número: 2010-079

Enunciado: No grafo G abaixo está destacado, em vermelho, um caminho de peso mínimo do vértice A ao vértice D (A->B->C->D). Se uma constante S for somada ao peso de cada aresta do grafo G, para quais valores de S o caminho A->B->C->D continuará sendo mínimo? E se cada aresta do grafo G for multiplicada por P, para quais valores de P o caminho A->B->C->D continuará sendo mínimo?

Assinale a alternativa contendo intervalos de valores de S e P que mantém a minimalidade do caminho A->B->C->D:

1. S ≥ 1 e P > 0.
2. S ≤ 1 e P > 1.
3. S ≥ 0 e P ≥ 0.
4. S > 2 e P ≥ 0.
5. NDA

Ideia original de: Fábio Augusto Faria

MO417 - Questão para a prova oral

Número: 2010-078

Enunciado: Observe o grafo orientado ponderado a seguir. Assinale a alternativa que contém uma afirmação correta em relação ao caminho mínimo (ou seja, de peso mínimo) a partir de uma origem u a um destino v, sendo u e v dois vértices distintos do grafo. Nota: caminhos podem repetir vértices.

1. Existe um caminho mínimo de A até G com peso positivo
2. Existe um caminho mínimo de B até C com peso igual a 10
3. Existe um caminho mínimo de A até D com peso igual a 20
4. Não existe um caminho mínimo de A até F
5. NDA

Ideia original de: Greice Martins de Freitas

MO417 - Questão para a prova oral

Número: 2010-076

Enunciado: No grafo orientado ponderado G a seguir, o valor dentro de cada vértice x indica o peso de um caminho mais curto da origem s até x. Assinale a alternativa CORRETA:


I. Existem oito árvores distintas de caminhos mínimos com raiz s.
II. Os valores de d[s], d[a], d[b], d[c] e d[d] são 0, -4, 4, -1 e 7, respectivamente.
III. Os valores de d[e], d[f] e d[g] são todos iguais a infinito.
IV. Não existem caminhos mais curtos, devido à existência de arestas de peso negativo e de ciclos no grafo G.

1. Todas as alternativas são corretas
2. Apenas II e III são corretas
3. Apenas III e IV são incorretas
4. Apenas IV é incorreta
5. NDA

Ideia original de: Priscila Tiemi Maeda Saito

MO417 - Questão para a prova oral

Número: 2010-074

Enunciado: Considere o grafo G=(V,E) mostrado na figura abaixo e seja C o corte definido pela curva em vermelho. Qual das alternativas abaixo é INCORRETA?

1. C respeita exatamente oito arestas de G.
2. Existe uma única aresta leve que cruza C.
3. (h,g) é uma aresta presente em todas as árvores espalhadas mínimas de G.
4. Pelo menos duas arestas que cruzam C devem fazer parte de qualquer árvore geradora mínima de G.
5. NDA

Ideia original de: Alexandre Toshio Hirata

MO417 - Questão para a prova oral

Número: 2010-073

Enunciado: Considerando a busca em profundidade realizada sobre o grafo a seguir, com os tempos de chegada e de partida apresentados em cada vértice, assinale a alternativa CORRETA:

1. I, II e III são arestas de árvore
2. IV é uma aresta cruzada
3. V é uma aresta de retorno
4. VI é uma aresta direta
5. NDA

Ideia original de: Priscila Tiemi Maeda Saito

MO417 - Questão para a prova oral

Número: 2010-072

Enunciado: Aplique o agoritmo de Prim para gerar uma árvore espalhada mínima no grafo abaixo. Qual das alternativas corresponde a duas possíveis sequências de seleção dos vértices?

1. (C, G, D, E, F, B, A) e (C, G, D, F, E, A, B)
2. (D, E, F, C, G, A, B) e (D, E, F, C, G, B, A)
3. (E, F, D, C, G, A, B) e (E, F, A, B, D, C, G)
4. (G, C, D, E, F, A, B) e (G, C, D, E, B, A, F)
5. NDA

Ideia original de: Alisson Pontes

MO417 - Questão para a prova oral

Número: 2010-070

Enunciado: Sabemos que encontrar caminhos de custo mínimo entre dois vértices num grafo é um problema fácil de se resolver. Porém, encontrar caminhos de custo máximo entre dois vértices é um problema difícil. O que podemos afirmar sobre árvores geradoras de custo máximo?

1. Não se conhecem algoritmos para encontrá-las em tempo polinomial
2. Podem ser encontradas com pequenas modificações nos algoritmos para árvores geradoras mínimas, mantendo a complexidade
3. Os algoritmos mais eficientes para este problema são bastante diferentes dos de árvore geradora mínima
4. Os algoritmos conhecidos que encontram árvores geradoras de custo máximo são polinomiais apenas para grafos esparsos.
5. NDA

Ideia original de: Pedro Henrique Del Bianco Hokama