MO417 - QUESTÃO PARA A PROVA ORAL
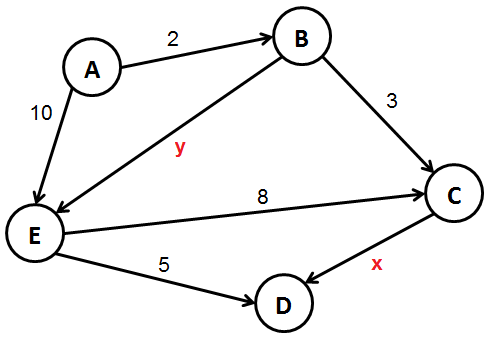
Número: 2013-109Enunciado: Você está jogando um jogo online chamado Danos. Percebendo que você pode converter o mapa do jogo em um grafo com vértices representando as posições no mapa e com arestas representando as passagens entre elas, você observa que cada aresta no grafo provoca uma quantidade de danos a você no jogo. É possível ainda representar os danos causados por pesos em cada aresta. Você então, usa o algoritmo de Dijkstra para encontrar o caminho de A a H, com o menor dano possível. Anote a ordem em que os vértices são removidos da fila de prioridade ao executar o algoritmo de Dijkstra.
- A, B, D, C, F, E, G, H
- A, B, C, D, F, E, G, H
- A, B, D, C, E, F, G, H
- A, B, C, D, E, F, G, H
- NDA
Ideia original de: Lucas Miguel de Carvalho
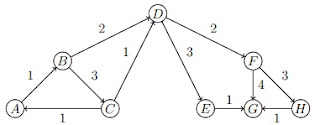




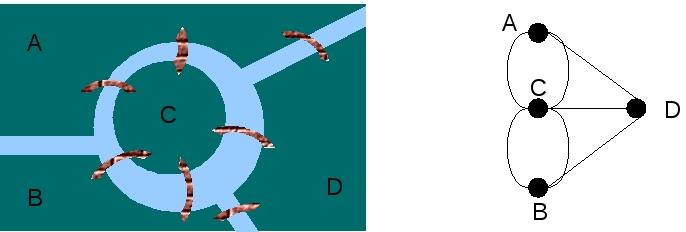
 III) Existe um único emparelhamento máximo no grafo acima.
III) Existe um único emparelhamento máximo no grafo acima.