MO417 - Questão para a prova oral
Número: 2013-079
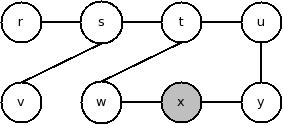
Enunciado: É dado o seguinte grafo direcionado com pesos descrito
por uma matriz de adjacências, em que uma entrada (i,j) diferente de 0
na matriz significa que há uma aresta de i para j.
a b c d
a| 0 -5 -3 0
b| 5 3 1 2
c| 4 -1 0 1
d| 0 0 2 0
a) -5 e -3Ideia original de: René du Raymond Sacramento
b) -3 e 6
c) -4 e -3
d) -1 e -6
e) N.D.A.
















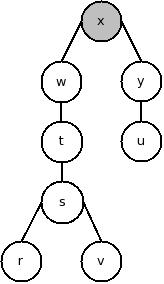
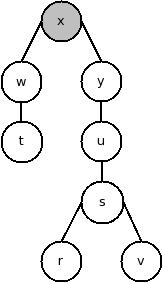
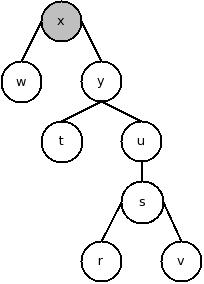
 I) Arestas de Árvore (que fazem parte de uma árvore de busca em profundidade).
I) Arestas de Árvore (que fazem parte de uma árvore de busca em profundidade).